Motivation

• Robot’s do not know the current state
• Sensors provide observations \(\mathbf{o}_i\) to be used to predict the state

State estimation: find a mapping from \(\{\mathbf{o}_i \}_{i=1}^n \mapsto \mathbf{x}\)

Sensors (for Flying Robots)

Inertial Measurement Unit (IMU)

Height (ToF)

Downward Optical Flow

Basic Complementary Filter

• Assume we can measure/compute part of the state directly
• Use a convex combination, weighing previous estimate \(\hat{\mathbf{x}}_{t}\) with the new measurement \(\mathbf{x}_m\): \[\begin{align} \hat{\mathbf{x}}_{t+1} = \alpha \hat{\mathbf{x}}_{t} + (1 - \alpha) \mathbf{x}_m,\quad \alpha \in [0,1] \end{align}\]

SO(3) Explicit Complementary Filter (ECF) by Mahony (Mahony, Hamel, and Pflimlin 2008; Euston et al. 2008)

• measured values are: \(\mathbf{o}_g\) (gyroscope) and \(\mathbf{o}_a\) (accelerometer)

• Use \(n(\mathbf{x}) = \frac{\mathbf{x}}{\| \mathbf{x}\|}\), and \(k_p, k_I \in \mathbb R\) tuning gains

• Each step, compute: \[ \begin{align} \mathbf{e}&= n(\mathbf{o}_a) \times \left(\mathbf{q}\odot \mathbf{e}_3 \right) & \delta &= k_p \mathbf{e}+ k_I \int \mathbf{e}\\ \dot{\mathbf{q}}_{next} &= \frac{1}{2} \mathbf{q}\otimes \overline{\mathbf{o}_g + \delta} & \mathbf{q}_{next} &= n(\mathbf{q}+ \dot{\mathbf{q}}_{next} \Delta t) \end{align} \]

• In words: Define the error as the cross product between measured gravity from the accelerometer and current estimate; use a PI controller to drive the error to zero.

• Sample implementation is here

SO(3) Complementary Filter by Madgwick (Madgwick 2014)

• Measured values are: \(\mathbf{o}_g\) (gyroscope) and \(\mathbf{o}_a\) (accelerometer)
• Step 1: Estimate \(\mathbf{q}\) from \(\mathbf{o}_a\) by solving: \[ \begin{align} \min_{\mathbf{q}}f(\mathbf{q}, \mathbf{o}_a) = \mathbf{q}^* \odot \mathbf{e}_3 - \frac{\mathbf{o}_a}{\|\mathbf{o}_a\|_2} \end{align} \]
  • In words: Find the rotation such that accelerometer frame and world frame align
  • Solve by gradient descent
• Step 2: Fuse gyroscope and accelerometer data \[ \begin{align} \dot{\mathbf{q}}_{next} &= \frac{1}{2} \mathbf{q}\otimes \overline{\mathbf{o}_g} - \beta\,n(J(\mathbf{q})^\top f(\mathbf{q}, \mathbf{o}_a))\\ \mathbf{q}_{next} &= n(\mathbf{q}+ \dot{\mathbf{q}}_{next} \Delta t) \end{align} \]
• Sample implementation is here

SO(3) Complementary Filter by Madgwick (Madgwick 2014)

• Efficient implementation needs analytical Jacobian

• Sympy demo: filter_madgwick.py

Complementary Filter UAV Summary

• Fuse measurements from different source or prior knowledge (convex combination, control gains, or gradient descent)

Background: Kalman Filter (KF) (Thrun, Burgard, and Fox 2005)

• Assume linear system dynamics with Gaussian white noise (process noise \(\mathbf{R}\)): \[ \begin{align} \mathbf{x}_{t+1} = \mathbf{A}\mathbf{x}_t + \mathbf{B}\mathbf{u}_t + \epsilon_t,\quad \epsilon_t \sim \mathcal{N}(0, \mathbf{R}) \end{align} \]
• Assume linear observations with Gaussian white noise (measurement noise \(\mathbf{Q}\)): \[ \begin{align} \mathbf{o}_{t} = \mathbf{C}\mathbf{x}_t + \delta_t,\quad \delta_t \sim \mathcal{N}(0, \mathbf{Q}) \end{align} \]

Background: Kalman Filter (KF) (Thrun, Burgard, and Fox 2005)

Background: Kalman Filter (KF) (Thrun, Burgard, and Fox 2005)

• Goal: Gaussian estimate of the state, i.e. the mean \(\mu\) and covariance \(\Sigma\).

• KF has two parts:

1. Prediction step: given the current estimate (\(\hat{\mathbf{x}}_t\) and \(\Sigma_t\)) and action \(\mathbf{u}_t\), compute a new estimate:

\[\begin{align} \hat{\mathbf{x}}_{t+1} &= \mathbf{A}\hat{\mathbf{x}}_t + \mathbf{B}\mathbf{u}_t\\ \Sigma_{t+1} &= \mathbf{A}\Sigma_t \mathbf{A}^\top + \mathbf{R} \end{align}\]

2. Measurement update: given the current estimate (\(\hat{\mathbf{x}}_t\) and \(\Sigma_t\)) and measurement \(\mathbf{o}_t\), compute a new estimate:

\[\begin{align} \mathbf{K}&= \Sigma_t \mathbf{C}^\top \left(\mathbf{C}\Sigma_t \mathbf{C}^\top + \mathbf{Q}\right)^{-1}\\ \hat{\mathbf{x}}_{t+1} &= \hat{\mathbf{x}}_t + \mathbf{K}(\mathbf{o}_t - \mathbf{C}\hat{\mathbf{x}}_t)\\ \Sigma_{t+1} &= (\mathbf{I}- \mathbf{K}\mathbf{C}) \Sigma_t \end{align}\]

Background: Kalman Filter (KF) (Thrun, Burgard, and Fox 2005)

Background: Extended Kalman Filter (EKF) (Thrun, Burgard, and Fox 2005)

• Generalize system dynamics and measurement model to: \[ \begin{align} \mathbf{x}_{t+1} &= g(\mathbf{x}_t, \mathbf{u}_t) + \epsilon_t,\quad \epsilon_t \sim \mathcal{N}(0, \mathbf{R})\\ \mathbf{z}_{t} &= h(\mathbf{x}_t) + \delta_t,\quad \delta_t \sim \mathcal{N}(0, \mathbf{Q}) \end{align} \]

Background: Extended Kalman Filter (EKF) (Thrun, Burgard, and Fox 2005)

Background: Extended Kalman Filter (EKF) (Thrun, Burgard, and Fox 2005)

Sympy demo: ekf.py

Background: Extended Kalman Filter (EKF) (Thrun, Burgard, and Fox 2005)

SO(3) Multiplicative Extended Kalman Filter (MEKF) (Markley 2003; Hall, Knoebel, and McLain 2008; Mueller, Hamer, and D’Andrea 2015)

• Split SO(3) state \(\mathbf{q}\) in error angle part (\(\boldsymbol{\delta}\in \mathbb R^3\)) and external absolute orientation part (\(\mathbf{q}_{ref}\))

\[ \begin{align} \mathbf{q}&= \mathbf{q}_{ref} \otimes \mathbf{q}(\boldsymbol{\delta}) \\ \mathbf{q}(\boldsymbol{\delta}) &= \begin{pmatrix} \cos(\| \boldsymbol{\delta}\| /2)\\ \frac{\boldsymbol{\delta}}{\| \boldsymbol{\delta}\|} \sin (\| \boldsymbol{\delta}\| /2) \end{pmatrix} \approx \begin{pmatrix} 1.0 - \| \boldsymbol{\delta}\|^2 / 8\\ \boldsymbol{\delta}/2 \end{pmatrix} \end{align} \]

• The filter state only contains \(\boldsymbol{\delta}\); \(\mathbf{q}_{ref}\) is treated as constant
• Add reset step, that recomputes \(\mathbf{q}_{ref}\)

SO(3) MEKF Prediction Step

• State: \(\mathbf{x}= [ \mathbf{p}, \mathbf{b}, \boldsymbol{\delta}]^\top \in \mathbb R^9\) (and \(\mathbf{q}_{ref}\) outside the filter)
  • \(\boldsymbol{\omega}\) can be directly observed and often remains not part of the EKF
  • \(\mathbf{b}\) is velocity in body frame (\(\mathbf{v}= \mathbf{q}\odot \mathbf{b}\)) (will simplify some math later!)
• Action: \(\mathbf{u}= [ \mathbf{o}_g, \mathbf{o}_a ]^\top\) (i.e., gyroscope and accelerometer are “actions” not measurements)
• Dynamics (step) \(\hat{\mathbf{x}}_{t+1} = g(\hat{\mathbf{x}}_t, \mathbf{u}_t)\): \[ \begin{align} \hat{\mathbf{p}}_{t+1} &= \hat{\mathbf{p}}_t + ((\mathbf{q}_{ref} \otimes \mathbf{q}(\hat{\boldsymbol{\delta}}_{t})) \odot \hat{\mathbf{b}}_t) \Delta t\\ \hat{\mathbf{b}}_{t+1} &= \hat{\mathbf{b}}_t + \left( (\mathbf{q}_{ref} \otimes \mathbf{q}(\hat{\boldsymbol{\delta}}_{t}))^* \odot \mathbf{g}+ \mathbf{o}_a \right) \Delta t\\ \hat{\boldsymbol{\delta}}_{t+1} &= \hat{\boldsymbol{\delta}}_{t} + \mathbf{o}_g \Delta t \end{align} \]

SO(3) MEKF Prediction Step

SO(3) MEKF Prediction Step

\[ \begin{align} \hat{\mathbf{x}}_{t+1} &= g(\hat{\mathbf{x}}_t, \mathbf{u}_t)\\ \mathbf{G}&= \frac{\partial g(\mathbf{x}, \mathbf{u})}{\partial \mathbf{x}} \vert_{\mathbf{x}=\hat{\mathbf{x}}_t, \mathbf{u}=\mathbf{u}_t}\\ \Sigma_{t+1} &= \mathbf{G}\Sigma_t \mathbf{G}^\top + \mathbf{R} \end{align} \]

SO(3) MEKF Reset Step

\[ \begin{align} \mathbf{q}_{ref} &= \mathbf{q}_{ref} \otimes \mathbf{q}(\boldsymbol{\delta}) \\ \boldsymbol{\delta}&= \mathbf{0} \end{align} \]

Optional: rotate \(\Sigma\) (Mueller, Hehn, and D’Andrea 2017)

Measurement Equation for Height

• \(\mathbf{o}_z = h(\mathbf{x}) = \mathbf{p}_z\) (for small \(\mathbf{q}\) w.r.t. FoV)

\[ \begin{align} \mathbf{H}&= \frac{\partial h(\mathbf{x})}{\partial \mathbf{x}} \vert_{\mathbf{x}=\hat{\mathbf{x}}_t}\\ &= \begin{pmatrix} 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \end{pmatrix} \end{align} \]

Measurement Equation for Flow

• outputs motion in pixels: \(\mathbf{o}_{xy} = [\Delta n_x, \Delta n_y ]^\top\)

\[ \begin{align} \mathbf{v}_m = \mathbf{q}\odot \begin{pmatrix} \frac{\mathbf{p}_z \theta_p}{N_p} \frac{\Delta n_x}{\Delta t}\\ \frac{\mathbf{p}_z \theta_p}{N_p} \frac{\Delta n_y}{\Delta t}\\ 0 \end{pmatrix} \end{align} \]

• \(\mathbf{o}_{xy} = [\Delta n_x, \Delta n_y ]^\top = h(\mathbf{x}) = \left( \frac{\Delta t N_p}{\mathbf{p}_z \theta_{p}} \left( (\mathbf{q}(\boldsymbol{\delta}) \otimes \mathbf{q}_{ref})^* \odot \mathbf{v}\right) \right)_{xy}\)

Measurement Equation for Flow

• \(\mathbf{o}_{xy} = [\Delta n_x, \Delta n_y ]^\top; h(\mathbf{x}) = \frac{\Delta t N_p}{\mathbf{p}_z \theta_{p}} \begin{pmatrix} \mathbf{b}_x\\\mathbf{b}_y\end{pmatrix}\)

\[ \begin{align} \mathbf{H}&= \frac{\partial h(\mathbf{x})}{\partial \mathbf{x}} \vert_{\mathbf{x}=\hat{\mathbf{x}}_t}\\ &= \begin{pmatrix} 0 & 0 & \frac{-N_p \mathbf{b}_x \Delta t}{\mathbf{p}_z^2 \theta_p} & \frac{N_p \Delta t}{\mathbf{p}_z \theta} & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & \frac{-N_p \mathbf{b}_y \Delta t}{\mathbf{p}_z^2 \theta_p} & 0 & \frac{N_p \Delta t}{\mathbf{p}_z \theta} & 0 & 0 & 0 & 0 \end{pmatrix} \end{align} \]

Large Matrices (and Embedded Systems)

• Matrix inversions are slow (roughly cubic)
• We have \(\left(\mathbf{H}\Sigma_t \mathbf{H}^\top + \mathbf{Q}\right)^{-1}\)
  • If \(\mathbf{H}\) has one row, the inversion becomes a division

MEKF Summary (1)

0. Initialize state \(\hat{\mathbf{x}}\), covariance \(\Sigma\)

1. On IMU update

   1. Reset: \[ \begin{align} \mathbf{q}_{ref} &= \mathbf{q}_{ref} \otimes \mathbf{q}(\hat{\boldsymbol{\delta}}) \\ \boldsymbol{\delta}&= \mathbf{0} \end{align} \]
   2. Convert \(\mathbf{b}\) to \(\mathbf{v}\)
   3. Predict \[ \begin{align} \hat{\mathbf{x}}_{t+1} &= g(\hat{\mathbf{x}}_t, \mathbf{u}_t)\\ \mathbf{G}&= \frac{\partial g(\mathbf{x}, \mathbf{u})}{\partial \mathbf{x}} \vert_{\mathbf{x}=\hat{\mathbf{x}}_t, \mathbf{u}=\mathbf{u}_t}\\ \Sigma_{t+1} &= \mathbf{G}\Sigma_t \mathbf{G}^\top + \mathbf{R} \end{align} \]

MEKF Summary (2)

2. On Measurement update

\[ \begin{align} \mathbf{H}&= \frac{\partial h(\mathbf{x})}{\partial \mathbf{x}} \vert_{\mathbf{x}=\hat{\mathbf{x}}_t}\\ \mathbf{K}&= \Sigma_t \mathbf{H}^\top \left(\mathbf{H}\Sigma_t \mathbf{H}^\top + \mathbf{Q}\right)^{-1}\\ \hat{\mathbf{x}}_{t+1} &= \hat{\mathbf{x}}_t + \mathbf{K}(\mathbf{o}_z - h(\hat{\mathbf{x}}_t))\\ \Sigma_{t+1} &= (\mathbf{I}- \mathbf{K}\mathbf{H}) \Sigma_t \end{align} \]

Unscented Kalman Filter (UKF) (Thrun, Burgard, and Fox 2005)

• Linearization using statistical linear regression
  • derivative-free
  • more computation (factor, not complexity)

Other Sensors

• Global Navigation System (e.g., GPS)
  • Measure directly absolute position \(\mathbf{p}\), easy to integrate
• Ultra-wideband ranging
  • Measure distance to known anchors, or other robots
  • Often used for indoor drone shows (e.g., Verity Studios)
  • Can be used for formation flight of multiple drones
• Lighthouse (HTC Vive)
  • Basestations (at known position) have a rotating laser (at known frequency)
  • Receivers can essentially use triangulation

Visual-Inertial Odomotry (VIO) (Scaramuzza and Zhang 2020)

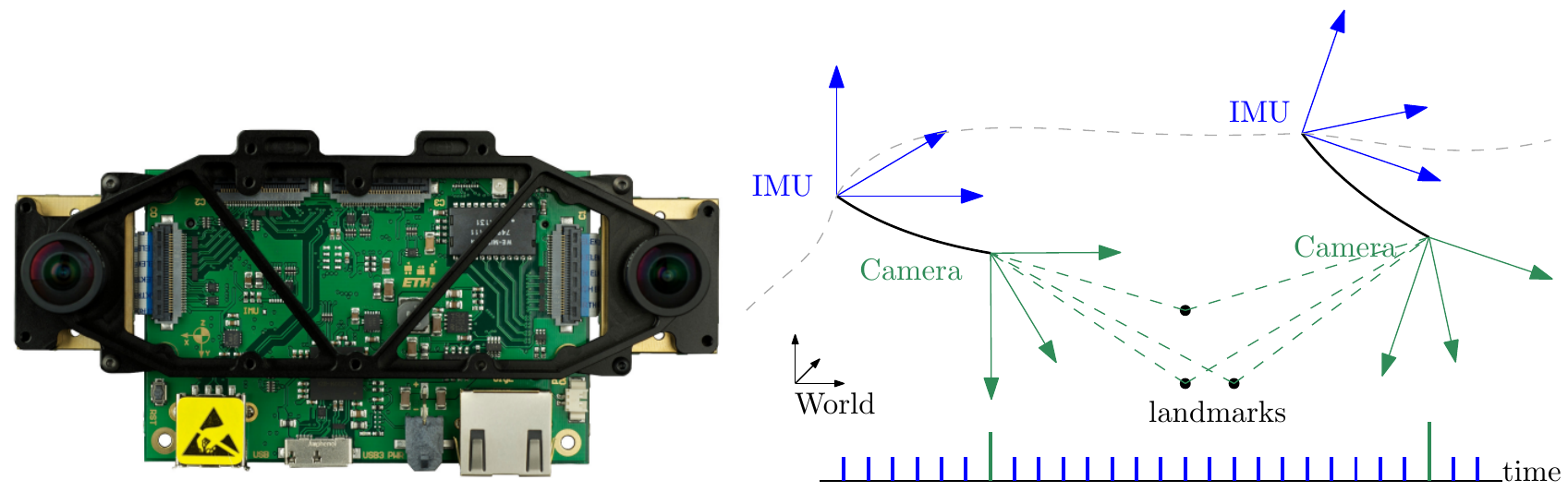
• Predict motion using IMU (integration)
• Predict motion using camera (typically using keypoints)
• Variants and more details in (Scaramuzza and Zhang 2020)

State Estimation in the Crazyflie Firmware

• Most state estimators
• EKF

Task

Implement the MEKF. Validate offline using the provided logging data and compare with the on-board EKF. Execute a physical test flight and qualitatively compare to the on-board EKF.

Variants:

1. Implement one of the complementary filters instead in simulation and physical flight (up to 15/20 points).
2. MEKF in simulation, complementary on-board (up to 18/20 points).

Simulation

• Given is a dataset of “our” figure-8 flight
  • reference estimate of the on-board EKF (\(\mathbf{p}, \mathbf{v}, \mathbf{q}\) over time)
  • Gyroscope over time (\(\mathbf{o}_g\) in deg/s !)
  • Accelerometer over time (\(\mathbf{o}_a\) in Gs !)
  • Height over time (\(\mathbf{o}_z\) in mm)
  • Flow over time (\(\Delta n_x, \Delta n_y\)) (needs to be swapped, flipped, done in conversion script)
• Given is a conversion script for *.csv (show example)
• Read the csv line-by-line
  • collect data that you need simultanously (e.g., gyroscope and accelerometer)
  • then call the appropriate function (e.g., mekf_predict)
  • write your output to a file, plot with e.g., Python

Physical Flight

• Sufficient to show it hover, using an existing (non-Rust) controller
• Approach:
  1. In app-config, add CONFIG_ESTIMATOR_OOT=y
  2. In lib.rs add estimatorOutOfTreeInit, estimatorOutOfTreeTest, and estimatorOutOfTree
  3. In the state estimator, use the following to loop over measurements

  let mut measurement = measurement_t {
      type_: 255,
      data: bindings::measurement_t__bindgen_ty_1 {
              gyroscope: bindings::gyroscopeMeasurement_t {
              gyro: bindings::Axis3f {
                  axis: [0.0, 0.0, 0.0],
              }}}};
  loop {
      unsafe {
          let ok = estimatorDequeue(&mut measurement);
          if !ok {
              break
          }
          let mut t = measurement.type_ & 0xFF; // the & 0xFF is important

Rust

• The MEKF requires different matrix sizes; Use generics to avoid code duplication

pub struct Mat<const Rows: usize, const Columns: usize> {
    pub m: [[f32; Columns]; Rows],
}

// Rows1xColumns1 X Rows2 x Columns2
// where columns1 == rows2
impl<const R1: usize, const C1: usize,
     const R2: usize, const C2: usize> 
    Mul<Mat<R2, C2>> for Mat<R1, C1> {
    type Output = Mat<R1, C2>;

    fn mul(self, other: Mat<R2, C2>) -> Mat<R1, C2> {
        // ...
    }
}

Timeline

• Jan 17: discussion/simulation presentation
• Jan 24: flight tests (no class meeting)
• Jan 31: Motion Planning lecture (& Assignment 4)

Learned Today

• State Estimation to estimate \(\mathbf{x}\) (and uncertainty)
  • Complementary Filter: simple, efficient, no dynamics model
  • Multiplicative Extended Kalman Filter: state-of-the-art state estimator for flying robots
• Assignment 3

Questions

References / Suggested Reading