About You

1. Field of Study
2. Robotics experience
3. Programming experience
4. Hopes/wishes for the course

Did anyone attempt this?

Lets present/discuss results and challenges!

Motors and Propellers

• We typically control the angular velocity of a motor \(\omega_i\) (in rpm)

Motors and Propellers

• Once we add a propeller, each motor/propeller creates a force (upward) and torque (in the direction of rotation)

\[ \begin{align} F_i &= \kappa_F \omega_i^2\\ \tau_i &= \kappa_\tau \omega_i^2 \end{align} \]

• Both relate quadratically to \(\omega_i\)
• \(\kappa_F\) and \(\kappa_\tau\) are found through system identification

Frame

• Motors are rigidly attached to a frame
• Common: X-configuration or +-configuration (here: X)

Force Allocation

• Mapping the control outputs (\(\omega_i\)) to the force \(f\) and body torque \(\boldsymbol{\tau}=(\tau_x, \tau_y, \tau_z)^\top\) (acting on the center of mass)

\[ \begin{align} \boldsymbol{\eta} = \begin{bmatrix}f\\\tau_x\\\tau_y\\\tau_z\end{bmatrix} = \mathbf B_0 \begin{bmatrix}\omega_1^2\\\vdots\\\omega_K^2\end{bmatrix} \end{align} \]

• \(\mathbf B_0 \in \mathbb R^{4\times K}\) is the allocation matrix

Allocation Matrix Example Plus-Configuration

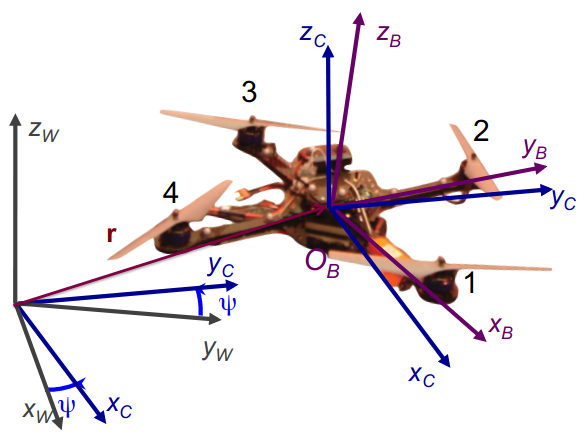
\[ \begin{align} \boldsymbol{\eta} = \begin{bmatrix}f\\\tau_x\\\tau_y\\\tau_z\end{bmatrix} = \begin{bmatrix} \kappa_F & \kappa_F & \kappa_F & \kappa_F\\ 0 & \kappa_F l & 0 & -\kappa_F l\\ -\kappa_F l & 0 & \kappa_F l & 0\\ \kappa_\tau & -\kappa_\tau & \kappa_\tau & -\kappa_\tau \end{bmatrix} \begin{bmatrix} \omega_1^2\\ \omega_2^2\\ \omega_3^2\\ \omega_4^2 \end{bmatrix} \end{align} \]

• \(l\): distance from the axis of rotation of the rotors to the center of the quadrotor

(From the seminal paper (Mellinger and Kumar 2011))

Reference Frame Crazyflie

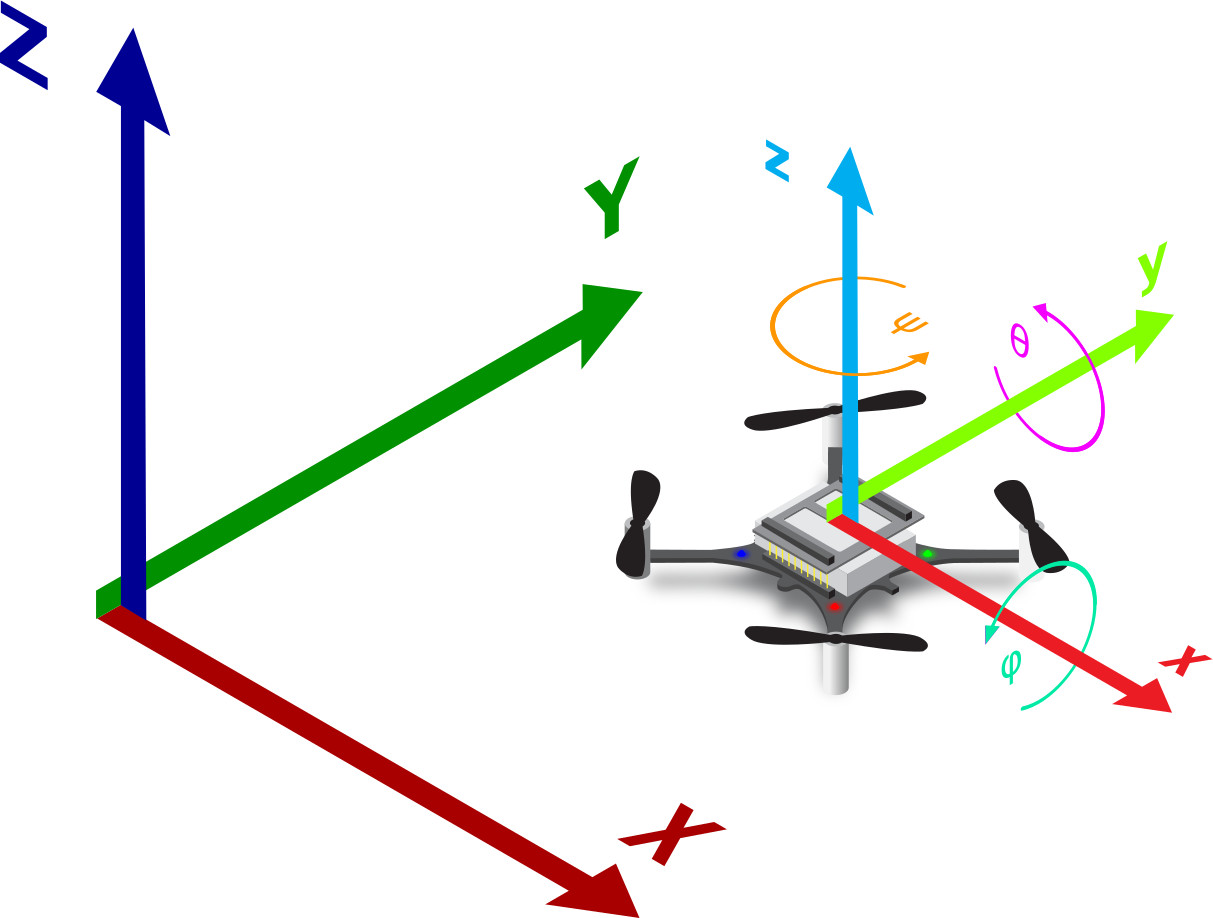
Allocation Matrix Crazyflie

\[ \begin{align} \boldsymbol{\eta} = \begin{bmatrix}f\\\tau_x\\\tau_y\\\tau_z\end{bmatrix} = \begin{bmatrix} \kappa_F & \kappa_F & \kappa_F & \kappa_F\\ -\kappa_F a & -\kappa_F a & \kappa_F a & \kappa_F a\\ -\kappa_F a & \kappa_F a & \kappa_F a & -\kappa_F a\\ -\kappa_\tau & \kappa_\tau & -\kappa_\tau & \kappa_\tau \end{bmatrix} \begin{bmatrix} \omega_1^2\\ \omega_2^2\\ \omega_3^2\\ \omega_4^2 \end{bmatrix} \end{align} \]

• \(a=\frac{l}{\sqrt{2}}\)

Flight Dynamics

Flight Dynamics

Flight Dynamics Challenges

• What’s the “skew-symmetric mapping”?

\[ \boldsymbol{\hat{\omega}} = \begin{bmatrix} 0 & -\omega_z & \omega_y\\ \omega_z & 0 & -\omega_x\\ -\omega_y & \omega_x & 0 \end{bmatrix} \]

• Not every \(3\times 3\) matrix is a rotation matrix
  • needs to be orthogonal
  • needs to have determinant 1

Rotation Representations

1. Rotation Matrix

2. Euler Angles

3. Quaternions

Quaternions

• A quaternion is represented as \(\mathbf q=(q_w, q_x, q_y, q_z)^\top=(q_w, \vec{\mathbf q})^\top \in \mathbb R^4\)
  • we denote \(\vec{\mathbf q}=(q_x, q_y, q_z)\)
  • we augment a point \(\bar{\mathbf r}\in\mathbb R^3\): \(\bar{\mathbf r} = (0, \mathbf r)^\top\)
• For rotations we have \[\mathbf q=\begin{pmatrix} \cos(\theta/2)\\ \mathbf u \sin (\theta/2) \end{pmatrix}\]
  • \(\theta\) is the rotation angle
  • \(\mathbf u\in\mathbb R^3\) is an axis
  • \(\| q \|_2 = 1\) (unit quaternion or normalized quaternion)

Quaternion Operations

• Negation: \[ -\mathbf q = (-q_w, -q_x, -q_y, -q_z)^\top \]

• Addition: \[ \mathbf q \oplus \mathbf p = (q_w + p_w, q_x + p_x, q_y + p_y, q_z + p_z)^\top \]

• Multiplication: \[ \mathbf q \otimes \mathbf p = \begin{pmatrix} q_w p_w - q_x p_x - q_y p_y - q_z p_z\\ q_x p_w + q_w p_x - q_z p_y + q_y p_z\\ q_y p_w + q_z p_x + q_w p_y - q_x p_z\\ q_z p_w - q_y p_x + q_x p_y + q_w p_z \end{pmatrix} \]

Quaternion Operations

• Conjugate \[ \mathbf q^* = (q_w, -q_x, -q_y, -q_z)^\top \]

• Norm: regular \(L_2\) norm on the vector \[ \| \mathbf q \| = \sqrt{q_w^2 + q_x^2 + q_y^2 + q_z^2} \]

Quaternion Vector Rotation

• With a rotation matrix \(\mathbf R\), we can rotate a vector \(\mathbf v\) as \[\mathbf v_{rotated} = \mathbf R \mathbf v\]

• With quaternion \(\mathbf q\) \[ \overline{\mathbf v_{rotated}} = \mathbf q \odot \mathbf v = \mathbf q \otimes \overline{\mathbf v} \otimes \mathbf q^* \]

(I.e., augment \(\mathbf v\) to a quaternion, use two quaternion multiplications, and one conjugate, and then extract the vector part of the result)

Quaternion Derivative

• Assuming \(\boldsymbol{\omega}\) in body frame (e.g., gyroscope): \[ \dot{\mathbf q} = \frac{1}{2} \mathbf q \otimes \overline{\boldsymbol{\omega}} \]

• Assuming \(\boldsymbol{\omega}\) in world frame \[ \dot{\mathbf q} = \frac{1}{2} \overline{\boldsymbol{\omega}} \otimes \mathbf q \]

Improved Quaternion Integration

• A rotation starting from \(\mathbf q_t\) with fixed angular velocity \(\boldsymbol{\omega}\) (body frame) for a (small) \(\Delta t\)

\[ \mathbf q_{t+\Delta t} = \mathbf q_t \otimes \begin{pmatrix} \cos{(\| \boldsymbol{\omega} \| \Delta t/2)}\\ \frac{\boldsymbol{\omega}}{\| \boldsymbol{\omega} \|} \sin{(\|\boldsymbol{\omega}\| \Delta t/2)} \end{pmatrix} \]

Quaternion References

More details and derivations at (Särkkä 2007; Jia 2024; Narayan 2017)

Flight Dynamics Reloaded

\[ \begin{align} &\dot{\mathbf{p}} = \mathbf{v}, && m\mathbf{\dot{v}} = m\mathbf{g} + \mathbf{q} \odot (0, 0, f)^\top,\\ &\dot{\mathbf q} = \frac{1}{2} \mathbf q \otimes \overline{\boldsymbol{\omega}}, && \mathbf{J}\dot{\boldsymbol{\omega}} = \mathbf{J}\boldsymbol{\omega}\times \boldsymbol{\omega} + \boldsymbol{\tau}_u, \end{align} \] where \[ \begin{align} \begin{bmatrix}f\\\boldsymbol{\tau}_u\end{bmatrix} = \mathbf B_0 \begin{bmatrix}\omega_1^2\\\vdots\\\omega_K^2\end{bmatrix} \end{align} \]

System Identification

• mass \(m\), arm length \(l\): scale, ruler
• inertia \(\mathbf J\): often estimated from CAD models
• motor and propellers: trust stand
  • for forces, this can be a scale where the UAV is mounted upside down
  • Example from 2015
  • Modern Commercial Thrust Stand

Modeling Wind

• In the dynamics, add an external force \(\mathbf{f}_a\)
  • might depend on time or location

\[ m\mathbf{\dot{v}} = m\mathbf{g} + \mathbf{q} \odot (0, 0, f)^\top + \mathbf{f}_a(\mathbf p, t) \]

Modeling Drag

• In the dynamics, also add additional force \(\mathbf{f}_a \propto \mathbf v\) and torque \(\boldsymbol{\tau}_a \propto \boldsymbol{\omega}\)

Rotor Placement

Dynamics Learning

• Difficult to model everthing
  • ground effect: a force when hovering close to the ground
  • interaction forces: forces when two UAVs are in close (vertical) proximity
• Typical approach:
  1. Collect data
  2. Use supervised learning to train (residual) models

Examples: (Bauersfeld et al. 2021; Shi et al. 2022; Smith et al. 2023)

Existing Simulators

• Many: recent survey lists 44 (Dimmig et al. 2024)
  • Some are generic robotics simulators (Gazebo, MuJoCo, Webots, Isaac Sim)
  • Some are highly specialized (e.g., for training RL agents)

Task

The goal of this assignment is to build a dynamics simulator for the Bitcraze Crazyflie 2.1 robot. This simulator will be extended in the upcoming assignments to test controls, state estimation, and motion planning.

Experiment on Simulation Quality

Compare (runtime/step size/solution quality) of two different integration schemes you have learned. Options:

1. Pure Euler integration,
2. Pure RK4 integration,
3. Exponential map for quaternion integration, Euler otherwise
4. Exponential map for quaternion integration, RK4 otherwise

Dynamics Validation

Given: state and action sequence of a sample flight.

Goal: Verify that the dynamics are correct.

Rust Hint: Operator Overloading

use std::ops::Add;
#[derive(Debug, Copy, Clone)]
struct Vec3 {
    x: f32,
    y: f32,
    z: f32,
}

impl Add for Vec3 {
    type Output = Self;

    fn add(self, other: Self) -> Self {
        Self {
            x: self.x + other.x,
            y: self.y + other.y,
            z: self.z + other.z,
        }
    }
}

fn main() {
    let a = Vec3 {x: 0.0, y: 1.0, z: 2.0};
    let b = Vec3 {x: 3.0, y: 4.0, z: 5.0};
    let c = a + b;
    println!("{:?}", c);
}

Learned Today

• Multirotor dynamics
• Efficient and numerically stable handling of rotations via quaternions
• Outline of Assignment 1

References / Suggested Reading

Questions